こんにちは。しらこです。
今回は、「数学的帰納法」のお話…。
数学的帰納法(すうがくてききのうほう、英: mathematical induction)は証明の手法の一つ。自然数に関する命題 P(n) が全ての自然数 n に対して成り立つ事を証明するために、次のような手続きを行う[注 1]。
1. P(1) が成り立つ事を示す。
2. 任意の自然数 k に対して、「P(k) ⇒ P(k + 1)」が成り立つ事を示す。
3. 1と2の議論から任意の自然数 n について P(n) が成り立つ事を結論づける。

この記事を読み終える頃には、↑の私みたいになっているはず…!!
…と言う事で、例題を交えて、解説していきます。
数学的帰納法とは?
例題

白と黒の石が、一列に、いくつか並んでいます。
"黒の次は黒"というルールです。
最初の石が"黒"なら、最後の石は、何色でしょう?
解答


当たり前だし、簡単簡単!!♫

この推論のことを、
"数学的帰納法"
と言うんだ。

これが"数学的帰納法"!?
(簡単すぎんか…!?)
はい。簡単でしょう?
でも、これだけでは、誤解の恐れがあるので、解説していきます。

誤解しないよう、解説していくよ。
解説
最初と、ルールが分かれば、あとは"これ!!"って推論できるもの
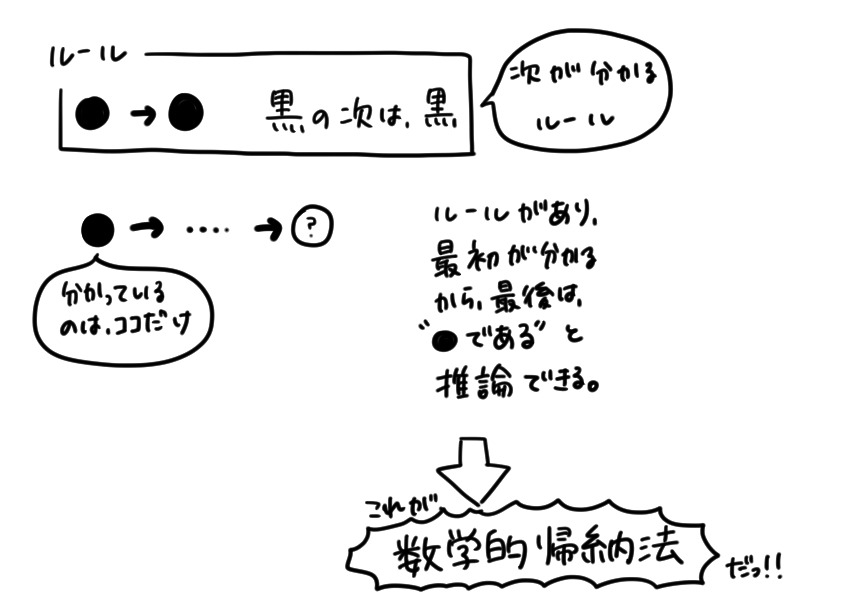
2つの条件が揃えば、あとは全て分かる
と推論したものである。
数学的帰納法ではない例題
男女何人かが、一列に並んでいます。
「男の子の次は、男の子」というルールです。
最初が女の子の場合、最後は男女どちらでしょう??
答えは「分かりません」。
この時、「男の子の次が男の子なら、女の子の場合でも、次が女の子だろう」と、思い込むことはできます。(←推論ではない。)
最初が男の子であれば、ルールに則り、最後も「男の子」と推論できることが、"数学的帰納法"であって、
最初が女の子であれば、「女の子もそうなるだろう」と予想するのは、数学的帰納法ではありません。
だって、女の子の情報は、一切書いてないんだもの。

あくまでも、"最初"と、"ルール"が分かれば、全て分かると推論できるものが、"数学的帰納法"になります。
数学的「帰納」法という名前がつけられているが、数学的帰納法を用いた証明は帰納ではなく、純粋に自然数の構造に依存した演繹論理の一種である。
数学的帰納法は、"帰納法"って名前に入ってるけど、一般的な"帰納法"とは、違うよ。
混同しないようにね。
数学的帰納法は、たった2つの条件さえわかっていれば、後は全て推論できる…という演繹なのです。
演繹(えんえき、英: deduction)は、一般的・普遍的な前提から、より個別的・特殊的な結論を得る論理的推論の方法である。
「人は必ず死ぬ」という大前提、「ソクラテスは人である」という小前提から「ソクラテスは必ず死ぬ」という結論を導き出す。この例のように二つの前提から結論を導き出す演繹を三段論法という。
数学は全て、演繹で議論されています。
(ただし、帰納的な(こうなるだろう…という予測から、普遍的にそうなる、と、示すことはあります。)



現代数学では、いくつかの公理から出発して議論を展開しているんだよ。

私が、当たり前だと思っていた"数学的帰納法"。
コウ(娘)に問題を出したところ、よく分かっておらず、コウにとっては、全然当たり前ではありませんでした…。

あのねぇ、コウちゃんねぇ、白いご飯が大好きなの〜💕
数学って面白いね

この辺りにも面白い話はいっぱいあってね、
球体を分割・組み替えて、同じ半径の球体を2個作ることができるんだ。
バナッハ・タルスキーの逆理って言うんだけど…。

どーゆーこと???
どーなってんの????
…ということで、面白い話はまだまだありますが、この辺で…。

数学って、面白いね。

今回の話で、数学って面白いよね。…っていう事が、ちょっとでも、伝わればいいな。

我が家は夜ご飯に食べるよ。皆さま、よいお年を〜!!
最後まで読んでいただき、また、本年もありがとうございました。
明日から2022年!!
冬休みの為、漫画も、数回、お休みしようと思っています。
来年も、ほっこりをお届けしていきたいと思っておりますので、よろしくお願い致します。