こんにちは。しらこです。
前書き
この漫画は、小2すんのテストを発端に、おいたんから聞いた話が面白かったので、描き始めました。
当初は
①小2すんのテスト
②掛け算の定義
③定義から可換は自明ではない(4話目がココ)
④非可換のおもしろい例
⑤物理のおもしろい話
⑥同型、同値な定義
⑦掛け算が可換は当たり前
⑧当たり前とは(公理)
⑨まとめ
という流れでした。
掛け算順序問題が、ここまで大きな問題であることを知らず、配慮に欠けた構成になっていました。
私としては、掛け算順序の議論に入っていくつもりはありませんでした。
掛け算順序固定の意義があるかどうかは、この漫画の主旨ではありません。
描くのが遅く、長くなりそうなので、このままでは誤解を広める可能性もあるため、構成を変えて、⑥⑦⑧あたりの漫画を描いて、一旦締めようと思います。
サクランボの例
全部で何粒あるでしょう?

↑この、サクランボの実、房から外して、並べると…↓
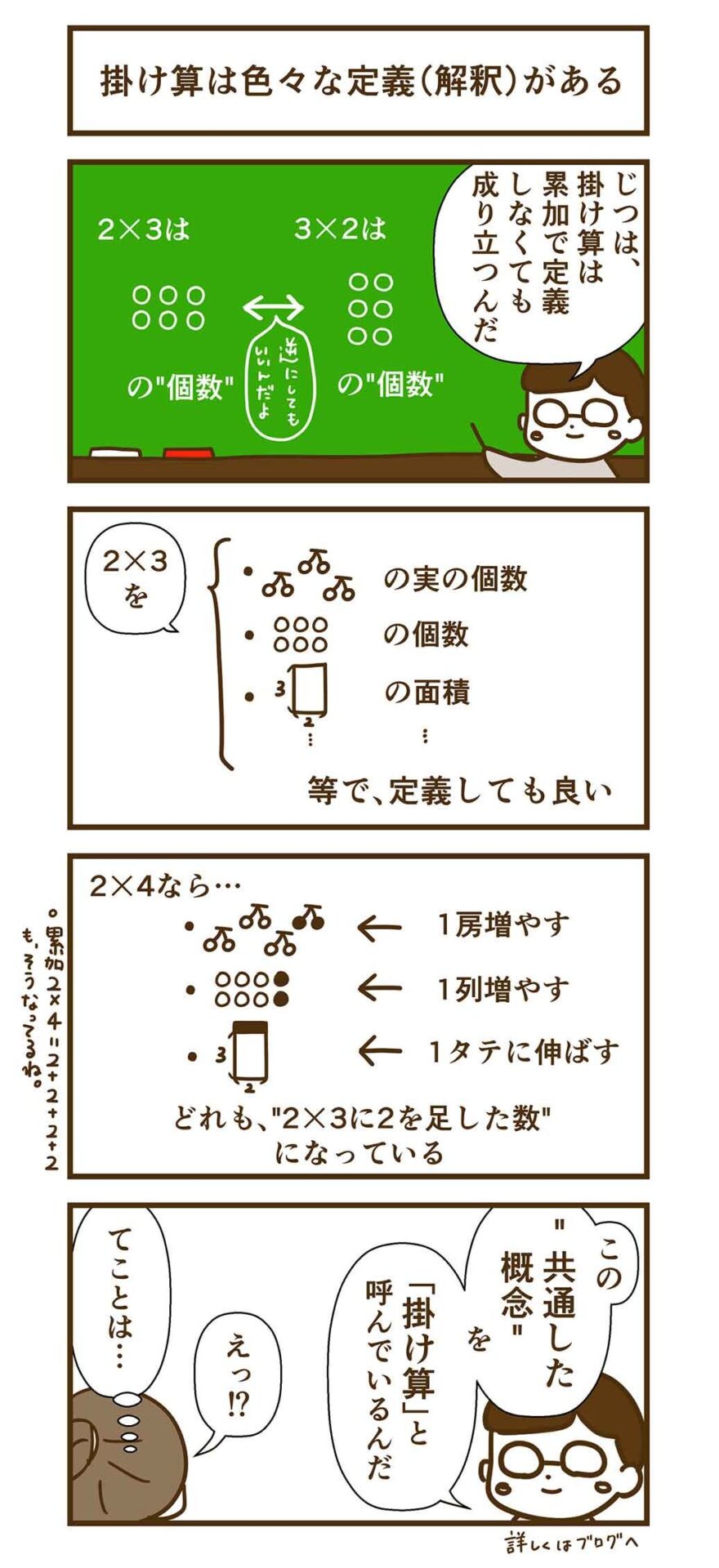
「2×3」を、このような並びの○の個数、と見る事もできる。
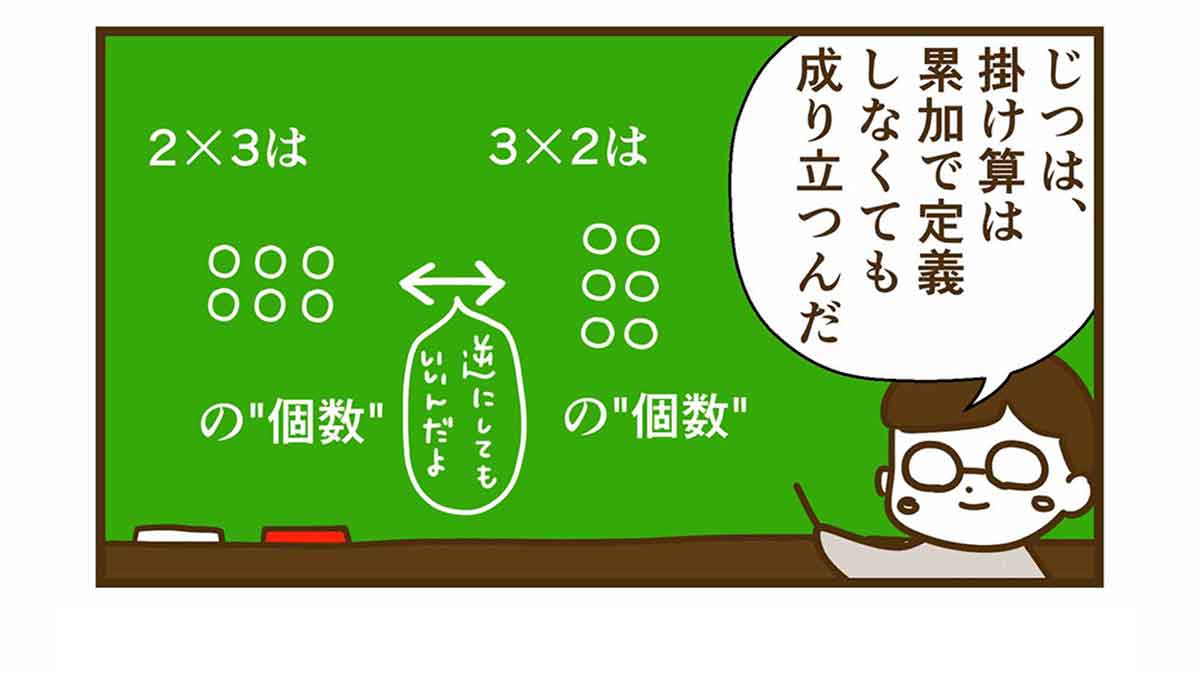
そしてこれは、
のように、色々な方法、考え方で定義しても良い。

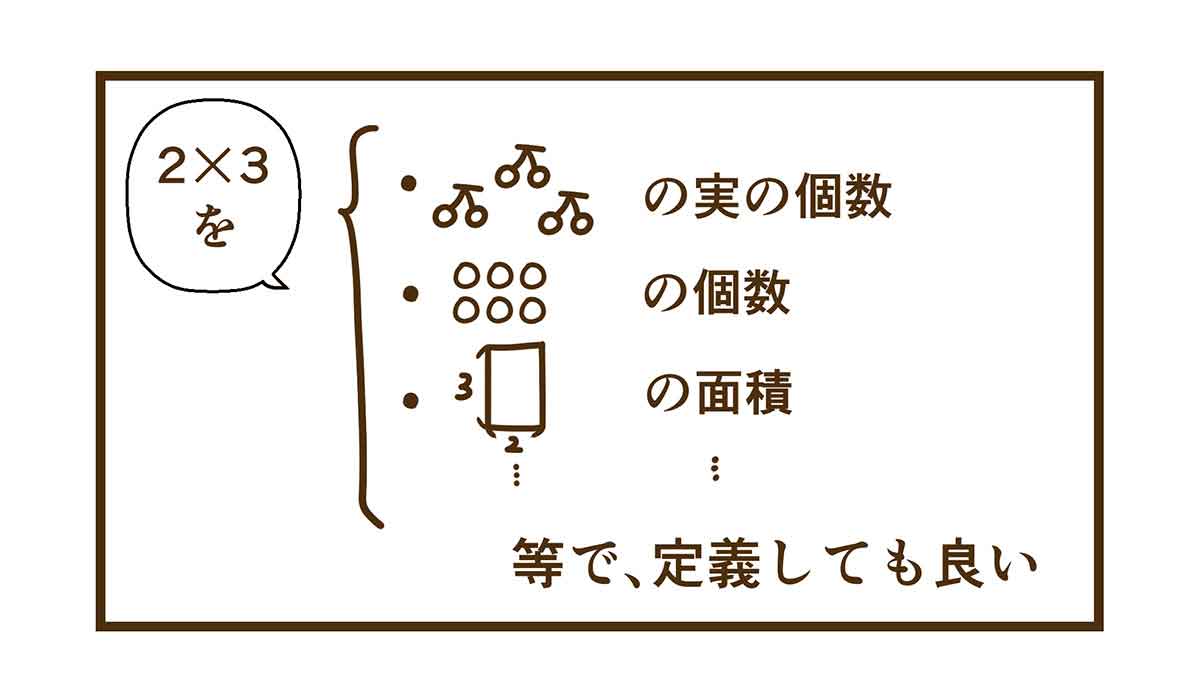
こう定義すると、「2×4」は、



色々な捉え方があるんだね!!

縦から数えた総数をn×mとすると、横から数えた総数がm×n。
「縦」は、どっちが「縦」であってもよく、どちらかが「縦」なら、どちらかが「横」となる。
※必ずしも、このような定義をしなければならないという訳ではありません。


全体の数は、どこからどう数えても「同じ」。
どちらか一方を「縦」としたら、もう一方は「横」として、数える。
この、「縦」と「横」は、どっちがどっちでもいいよね?

…と、そこに疑問を持って、どうだろうか?と考えることも、数学なんだよ。

なんか、分かってきたぞ!!
数学って、そう言う事なんだね!!

次回予告

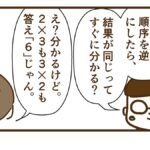
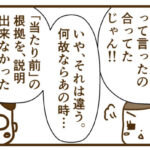
「41×17」も「17×41」も、「同じ!!」って言ったの、合ってたじゃん!!

何故なら…(続く)
(漫画を描くのが追いついていないので、台詞で…。↑次の1コマ目のやりとりです。)
コウ(娘)の誕生日プレゼント↑。
めちゃくちゃ喜んでくれました(^^)

掛け算順序6話目はこちら