<注意>
これは、小2すん(息子)のテストが発端となり、おいたん(兄)から聞いた話が面白かったので、漫画にしました。
ここだけ(4話目だけ)見ると、誤解が生じる恐れがあるので、是非、最後まで読んでいただければと思います。
学校教育に関する議論とは、無関係です。
![]()
これは、小2すん(息子)のテストが発端となり、おいたん(兄)から聞いた話が面白かったので、漫画にしました。
ここだけ(4話目だけ)見ると、誤解が生じる恐れがあるので、是非、最後まで読んでいただければと思います。
学校教育に関する議論とは、無関係です。

こんにちは。しらこです。
前回のお話で、
掛け算の順序を考えることは、文章問題を解くのに役立つだろう
ということが分かりました。
そして今回は、
掛け算の順序は数学的に大事だよ
というお話をします。

私
私的には、「数学的に大事」…っていう言葉の意味がよく分からんのだけど、こういう意味で大事なことが、「数学的に大事」っていうことなんだなぁ〜と思ったよ。
【注意】
「掛け算の順序が数学的に大事」というのは、
"掛け算を累加で定義すると、掛け算が可換(交換可能)である事は自明ではない(当たり前ではない)"という意味で、数学的に大事だよ。という事です。
決して、掛け算の順序を守る事が、数学的に大事という意味ではありません。


おいたん
掛け算の順序を逆にしたら、結果が同じっていうのは、すぐに分からんよね?

私
え?分かるけど。
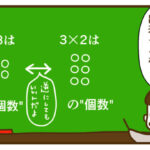
「2×3」も「3×2」も答え「6」じゃん。
(何言ってんの?)
「2×3」も「3×2」も答え「6」じゃん。
(何言ってんの?)
掛け算は入れ替えても答えが同じって、すぐ分かる?


おいたん
それは「2×3」という数字が小さくて、すぐ計算出来ているからだよ。
じゃあ、2桁の掛け算の問題を出そう。
「41×17」と「17×41」の結果が同じになるって、一瞬で分かる?
じゃあ、2桁の掛け算の問題を出そう。
「41×17」と「17×41」の結果が同じになるって、一瞬で分かる?

私
えっ??
41と17を入れ替えただけやん。答えが一緒になるに決まっとるやん。
(はぁ?何言っちゃってんの、この人?ますます意味分からんけど…)
41と17を入れ替えただけやん。答えが一緒になるに決まっとるやん。
(はぁ?何言っちゃってんの、この人?ますます意味分からんけど…)
(ここ、私が理解するのに一番苦労したところでした…)
「掛け算が可換(交換可能)である」と知っているに過ぎない


おいたん
それは、「掛け算を入れ替えても結果が同じ」ということを知っているだけ。
これから掛け算の勉強をしようとする人たちは、そんなことは知らないんだよ。
「41×17=17×41」を証明するには、計算するでしょ?
これから掛け算の勉強をしようとする人たちは、そんなことは知らないんだよ。
「41×17=17×41」を証明するには、計算するでしょ?

私
やっぱり、何言ってんのか分からない…
「41×17」と「17×41」は見た目は同じ?

おいたん
じゃあ、「41×17」と「17×41」は見た目は同じ?
「2×3」と「3×2」でもいいけど、これは、見た目は同じ?
「2×3」と「3×2」でもいいけど、これは、見た目は同じ?

私
(えっ?見た目??)
(数字入れ替えただけでしょ?一緒じゃん!!)
同じ!!
(数字入れ替えただけでしょ?一緒じゃん!!)
同じ!!

おいたん
いやいや、違うやろ?
数字、入れ替わっとるやろ??
数字、入れ替わっとるやろ??

私
まぁ確かに数字は入れかわっとるけれども…

おいたん
ちょっと今、答えいくらになるか、計算してみて。

私
(電卓ポチポチ)
(どっちも)697!!
(どっちも)697!!

おいたん
今、電卓使ったでしょ?
電卓で、計算したでしょ?
「41×17」と「17×41」が同じ数になるか、電卓で「確認」したでしょ?
これ、掛け算を知らない人たちは、どうやって確認すると思う?
今、掛け算は足し算で定義しているから、1つずつ足していって、確認していくしかないんだよ。
電卓で、計算したでしょ?
「41×17」と「17×41」が同じ数になるか、電卓で「確認」したでしょ?
これ、掛け算を知らない人たちは、どうやって確認すると思う?
今、掛け算は足し算で定義しているから、1つずつ足していって、確認していくしかないんだよ。
【掛け算の順序2話目】で、「掛け算は累加(足し算)」と定義したので、「41×17」と「17×41」は、

↑こうなる。
この足し算、見た目が同じですか?一瞬で、計算できますか?

私
見た目は全然違うし、一瞬で計算もデキマセン…
計算してみて初めて「イコール」で結べる


おいたん
41×17を計算するとき、足し算してるでしょ?
掛け算を足し算で定義してるから、
「41×17」は、「41を17回」足して計算するんだよ。
答えが「697」だったね。
逆も同じ。「17を41回」足して、答えが「697」だと分かる。
「41×17」と「17×41」の、どちらも数えてみたら「697」と、数が同じになったから「=」で結べたんだよ。
掛け算を足し算で定義してるから、
「41×17」は、「41を17回」足して計算するんだよ。
答えが「697」だったね。
逆も同じ。「17を41回」足して、答えが「697」だと分かる。
「41×17」と「17×41」の、どちらも数えてみたら「697」と、数が同じになったから「=」で結べたんだよ。

私
なるほどね〜

おいたん
掛け算が可換(交換可能)って、どうやって知ったか覚えてる?
まず、九九を覚えるよね?その時に、九九の中の数字は、入れかえても答えが同じなんだな、と、知る。
九九の中の数字を入れかえても、「A×B=B×A」になってるから、「掛け算は交換可能」と思ってるに過ぎないんだ。
学校のドリルとかで何回もやっているうちに、「掛け算は数字を入れ替えても同じ答え(数字)が出てくる」と推測して、それが当たり前になる。
実際、掛け算は交換可能だしね。
だけど、A×B=B×Aは本当に成り立つの?と言われたら、証明しないと分からないんだ。
まず、九九を覚えるよね?その時に、九九の中の数字は、入れかえても答えが同じなんだな、と、知る。
九九の中の数字を入れかえても、「A×B=B×A」になってるから、「掛け算は交換可能」と思ってるに過ぎないんだ。
学校のドリルとかで何回もやっているうちに、「掛け算は数字を入れ替えても同じ答え(数字)が出てくる」と推測して、それが当たり前になる。
実際、掛け算は交換可能だしね。
だけど、A×B=B×Aは本当に成り立つの?と言われたら、証明しないと分からないんだ。

私
そっか〜。なるほどね〜。
私は、「掛け算が交換可能」って知っていて、それが当たり前だと思っていただけなんだねぇ〜。
私は、「掛け算が交換可能」って知っていて、それが当たり前だと思っていただけなんだねぇ〜。

おいたん
そうそう。
しらこが主張してたのは、三角形の合同の問題で、「△ABCと△DEFが、合同になることを証明せよ」って言ってるのに、「合同になるのを知っているから、その三角形は合同になるに決まってる」って言っているようなもの。
しらこが主張してたのは、三角形の合同の問題で、「△ABCと△DEFが、合同になることを証明せよ」って言ってるのに、「合同になるのを知っているから、その三角形は合同になるに決まってる」って言っているようなもの。

私
そっかぁ〜。
掛け算を累加で定義すると自明ではない(証明が必要)って意味が、ようやく分かったよ。
累加で定義しただけでは、それが可換かどうか、見た目違うし、分からないよねぇ。
掛け算を累加で定義すると自明ではない(証明が必要)って意味が、ようやく分かったよ。
累加で定義しただけでは、それが可換かどうか、見た目違うし、分からないよねぇ。

私
でもさ、掛け算を足し算で定義すると証明が必要だよ。って話、
小学生には難しくない?
私だって、「証明せよ」って言われても、どうすれば良いか分からないし…。
小学生には難しくない?
私だって、「証明せよ」って言われても、どうすれば良いか分からないし…。

おいたん
そうだね。
小学生に証明せよ。なんて言わないでしょ。
でもこういうところが、数学の面白いところでもあるんだ。
小学生に証明せよ。なんて言わないでしょ。
でもこういうところが、数学の面白いところでもあるんだ。

おいたん
それに掛け算は実は…続く。

私
うつぼ屋さんと言えば、「坊っちゃん団子」。
だけど私は、坊っちゃん団子より、しょうゆ餅が好き。
美味しいよ。
だけど私は、坊っちゃん団子より、しょうゆ餅が好き。
美味しいよ。

私
ではまた〜!!