これは、小2すん(息子)のテストが発端となり、おいたん(兄)から聞いた話が面白かったので、漫画にしました。
ここだけ(3話目だけ)見ると、誤解が生じる恐れがあるので、是非、最後まで読んでいただければと思います。
学校教育に関する議論とは、無関係です。

こんにちは。しらこです。
掛け算の順序3話目。
何故、掛け算の順序が大事なのか?
それは、教育的観点から大事になります。
<注意>
“まとまりの数”の取り扱いが苦手な人にとっては、大事になる場合もある…というお話です。
勿論、"まとまりの数"の取り扱いが苦手であっても、掛け算の順序を固定する必要がない人はいるので、万人に通用するものではありません。


(何のこっちゃ…)
「概念」は、「それはどういうものか」についての共通の認識を指します。

例題
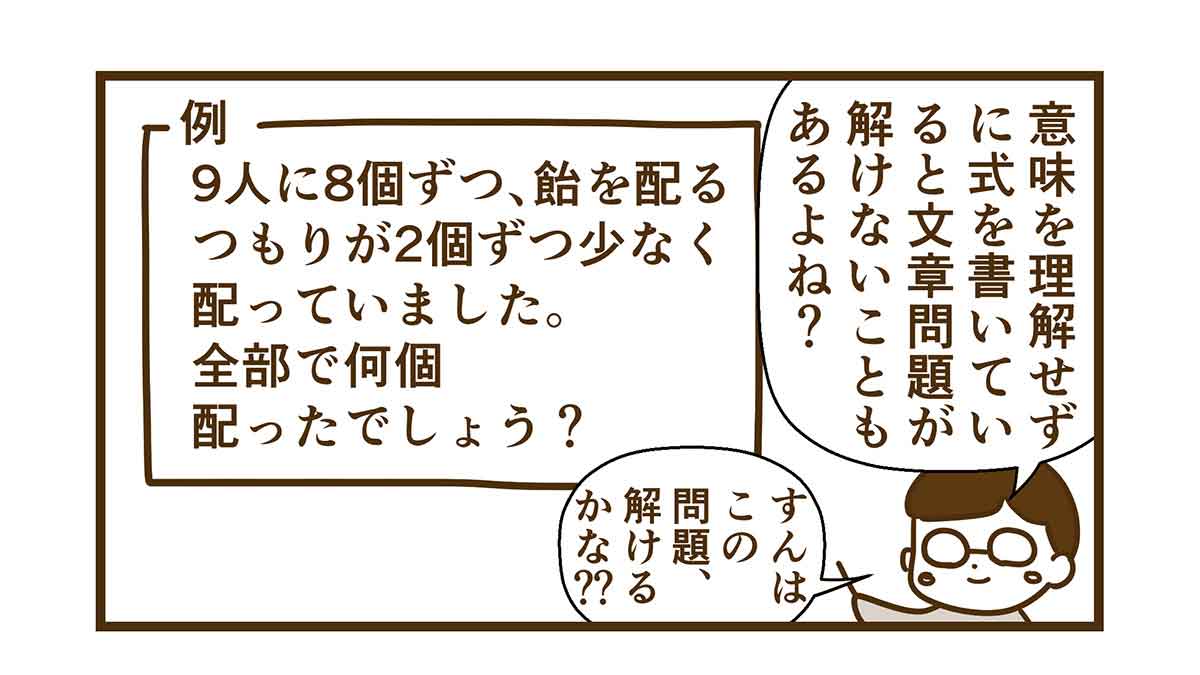
飴を8個ずつ配るつもりが、2個ずつ、少なく配りました。
全部で、何個の飴を配ったでしょう?
自分の子供が、テストやプリントで、掛け算の順序に「バツ」が付けられていた場合、上記の例題のような文章問題を出してみましょう。
(但し、上記の問題は高学年には簡単すぎるので、4/5分は何時間か?と言った問題を出してみてください。すぐに解けるようなら問題ありません。)

(実際は口頭で問題を出してみた↓)

問題っ!!ちゃちゃん!!✨
子供が9人います。
飴を8個ずつ配るつもりが、6個ずつ配ってしまいました。
飴は全部で何個配ったでしょう?



↑すん(息子)が書いたメモ。
すんはちゃんと理解してるっぽい。

このような問題が解けるなら問題ありません。
間違えるようなら、「この子はまだ理解してないな…」と思って、教えてあげて欲しいと思います。
補足
掛け算の順序を縛ることで、”まとまりの数”の概念の理解が進むのか?
おいたん曰く、

とのこと。
おはじきで、2のまとまりを3つ作る。
2+2+2

と言って「2×3」と教える(定義する)方が、初学者には分かりやすいのではと思います。
全ての学校でそのように教えているかは分かりませんが、少なくとも小2すんの母親である私は、そのように教えています。

表記の問題
「2+2+2」を「2×3」と書くか「3×2」と書くかは表記の問題であって、英語圏では「3×2」と書きます。
日本語を母語とする人であっても、そう捉える人は、いるかもしれません。
数(や抽象的な概念)を捉えられるようになる過程は一通りではなく、よく「言語ではこれ以上説明することができない」状態になります。
より複雑な方が理解を早める場合もあるので、どう理解を深めていくかは各個人で異なります。
(蛇足ですが、厳密には他者がある概念を理解しているかどうかを確認する術はありません。何度かの問答で「おそらく理解しているであろう」と言うことはできるかもしれませんが。)
掛け算の順序縛りは、道具の1つ
この掛け算順序縛りですが、まとまりの数の取り扱いを促す道具の1つ、くらいに捉えるのが良いのかもしれません。

中には補助輪が必要ない人もいるでしょう。
むしろこの補助輪が自転車に乗れるようになるのを妨げている、と考える人もいるでしょう。
でも、補助輪が必要な人もいるでしょう。

使っていると普通のお箸が持てなくなるとかいう意見もあるし。
でも「絶対必要ない」なんて、言い切れないもの。
繰り返しになりますが、掛け算順序縛りは”まとまりの数の取り扱いを促す道具の1つ”程度です。
子供の理解が深まるのなら、どんな風に教えても良いと思います。
次回予告



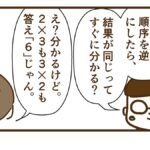
2×3も3×2も、答えは「6」じゃん。


知らなかった〜。
大人でも、お箸の正しい持ち方が、出来てなかったりするもんねぇ。

![学校は掛け算を[まとまりの数]×[個数]で教えている【掛け算の順序2話目】](https://snsnblog.com/wp-content/uploads/2021/12/1-1-1-150x150.jpg)