目次
こんにちは。しらこです。
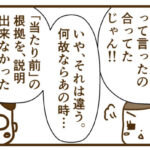
掛け算の順序について、漫画とブログを描いておりますが、
「掛け算は[まとまりの数]×[個数]で計算している【掛け算の順序2話目】」
で、一部、記載に誤りがありましたので、訂正して、お詫び申し上げます。
ごめんなさい…。
![学校は掛け算を[まとまりの数]×[個数]で教えている【掛け算の順序2話目】](https://snsnblog.com/wp-content/uploads/2021/12/1-1-1-150x150.jpg)
↑こちらの漫画、記事ともに、修正しました。
こちらの記事、なにがどう間違えていたのかというと…
小学校でこう習うのが当たり前だと思っていた
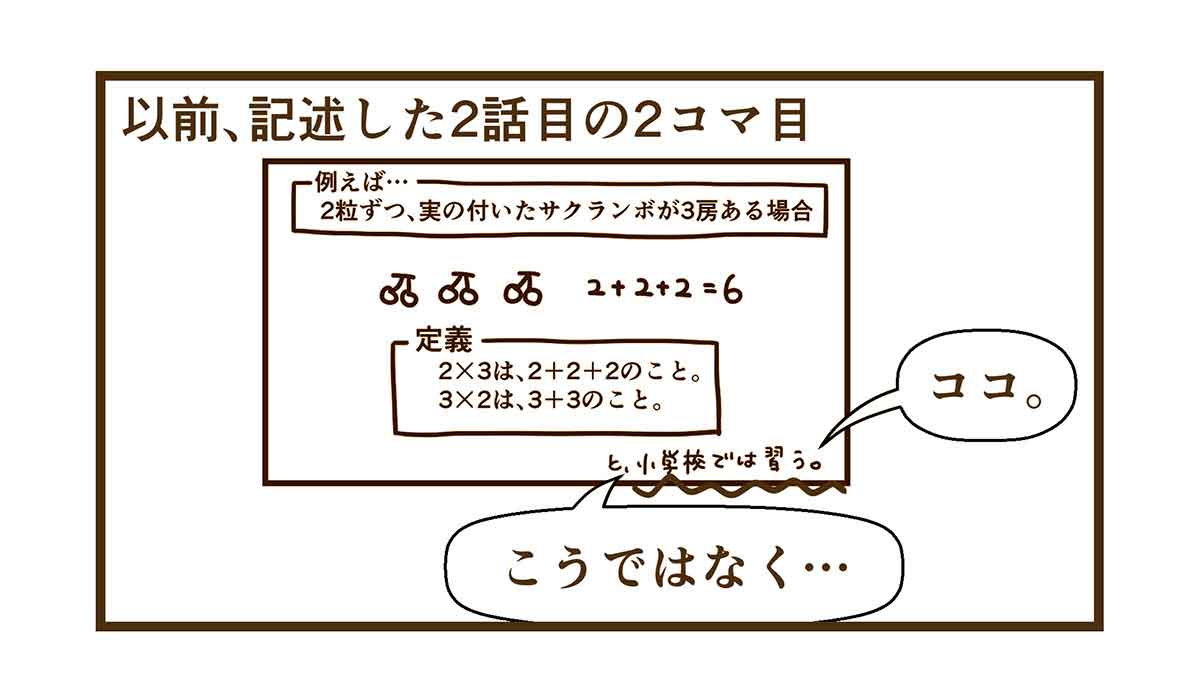
"小学校では習う"の部分…
実際、すん（息子）が使っている教科書には、
すんが使っている教科書2〜3ページ目
すんが使っている教科書4〜5ページ目
すんが使っている教科書6〜7ページ目
と、記載されていました。
私がこの教科書を確認した時、
と思い、「小学校では習う」と記載しました。
そしてこの記述が「教科書には載ってない！！」「デタラメだ！！」「人として恥ずかしい！！」などと人格否定までされる批判となったのです。
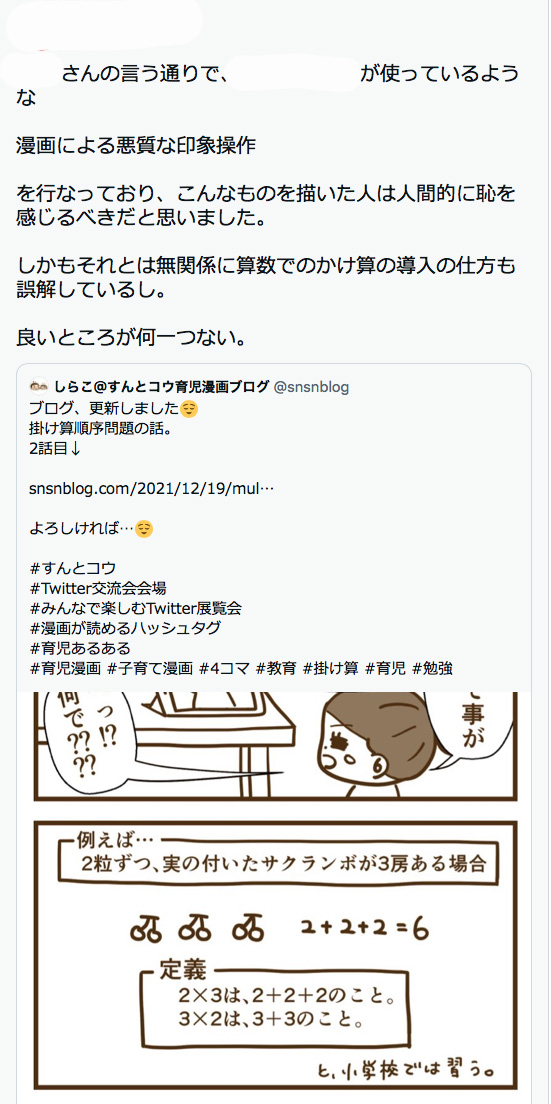
2×3は2＋2＋2の事と定義し、"小学校では習う"と記載してはダメなの？
そこってそんなに大事な事なの？？
この時点では、何故こんなにバッシングされているのか、分かりませんでした…。
↓そして、これ。
（※個人を晒したり、ここで批判する意図はないので、個人名を伏せています。）
ここでもう一度、教科書2〜7ページ目を見てみましょう。
すんが使っている教科書2〜3ページ目
↑まず、絵が描いてあります。
（かけ算の話には触れていません。）
すんが使っている教科書4〜5ページ目
↑かけ算は「1つ分の数」×「いくつ分」＝全部の数 のように書く。
「3×4」や「4×5」のような計算を、「かけ算」と言います。
すんが使っている教科書6〜7ページ目
↑問題文が並びます。
7ページ目に
かけ算の答えの求め方
3×5の答えは、3＋3＋3＋3＋3で、もとめることができます
と書かれている。
分かりますか？
教科書は、
かけ算を累加で定義している訳ではなく、かけ算を累加で求めることができる
…と、記載されています。
定義（ていぎ）は、一般にコミュニケーションを円滑に行うために、ある言葉の正確な意味や用法について、人々の間で共通認識を抱くために行われる作業。
教科書は"場面"、"シチュエーション"の記載になっている
かけ算を累加で定義している訳ではなく、かけ算を累加で求めることができると記載されている。
この違いが、何故こんなに重要なのか？それは…
"場面"や"シチュエーション"を表しているのではなく、
その時の"総数"、"数"であるから。
例題
3人に飴を2個ずつ配りました。飴は全部で何個配ったでしょう？
（※他にも考え方はあります）
この場合、かけ算は、どちらの考え方でも良いのですが、導入が"場面"であると、
とすると、
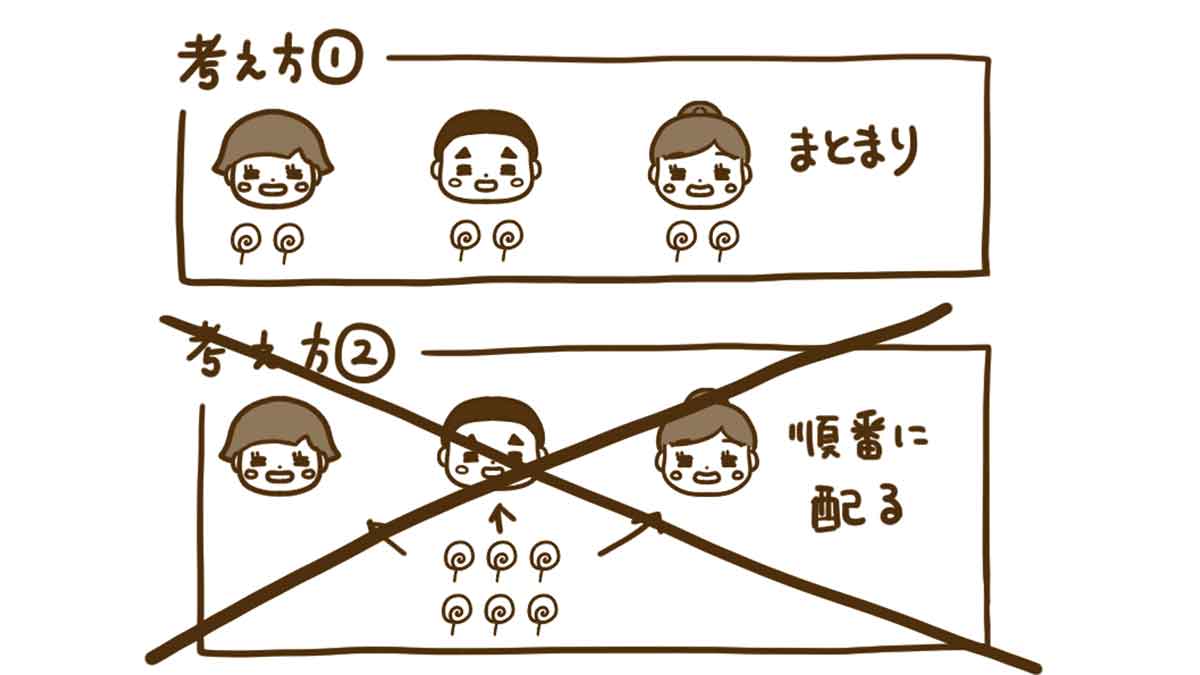
考え方②は、バツになってしまいます。
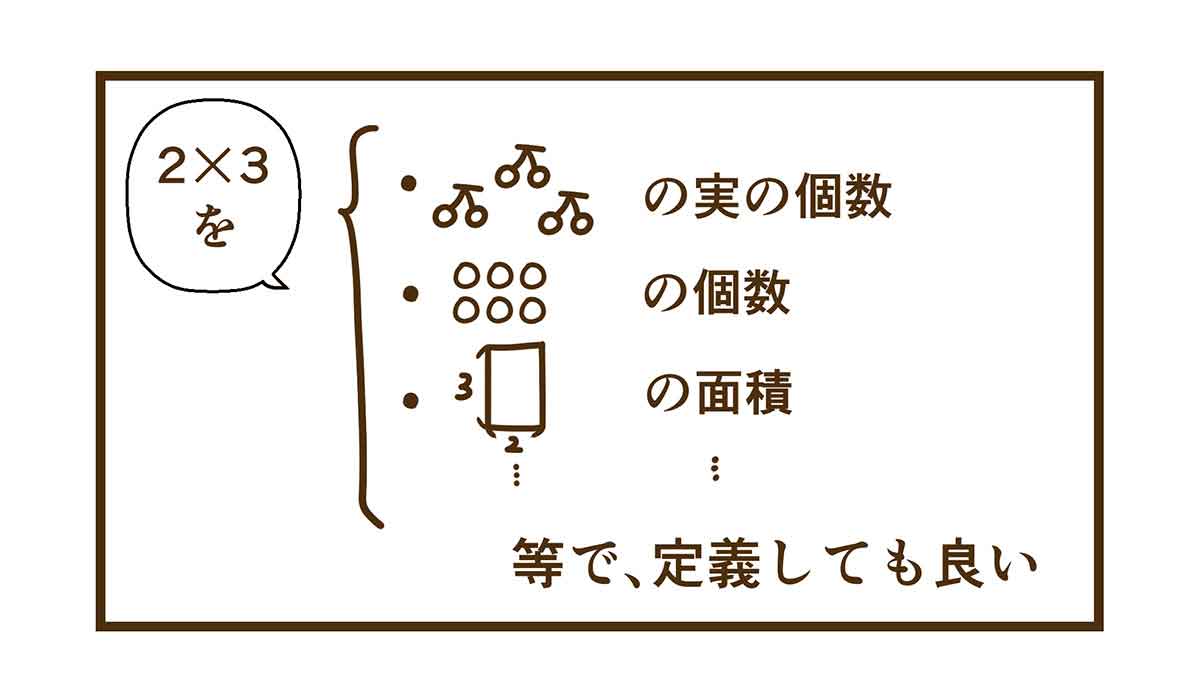
（↑前回のお話【掛け算順序5話目】の漫画より）
↑縦から見ても、横から見ても、どちらが縦でも横でもよいのが"かけ算"なのに、
"場面"や"シチュエーション"から導入すると、
"縦から考えなければならない"や"上から数えることがかけ算"のように、誤った認識になってしまう恐れがある。
もっと言うと、これが「みかんでなければならない」とか、「人でないといけない」等、式が"場面"を表す、という認識になってしまう可能性がある。
g（グラム）や、速度もかけ算なのに…。
そしてこれが非常に問題である（という指摘の）為、
↑教科書には、「小学校で習う」なんて書いてないよ。
ということでした。
すんと、そのお友達の認識
教科書の導入では、「かけ算を累加で定義する」という記載はありませんでしたが、
すん（息子）の話を聞くと、
「2×3は、2＋2＋2のこと」
という認識であり、
すんの友達（他のクラスの子）も、
「2×3=2＋2＋2と教えられた」という認識でした。
（他のクラスでは、宿題プリントに2＋2＋2＋2＋…、2が何個あるか？を数えて、2×○と書かせる問題が出ていたとのこと。）
しかし、先生が実際、掛け算を子供達にどう教えたのか？
ちゃんと定義したのか？板書は？と言われると、その時の授業を見ていた訳ではなく、記録が残っている訳でもないので、実際のところは分かりません。
あくまでも、すん（息子）や、すんのお友達が、
「2×3=2＋2＋2のこと」という認識である
というだけです。
申し訳ありません…。
改めて、お詫び致します
以上より、【かけ算順序2話目】の2コマ目に関して、私の認識が甘かったこと、
実際、教育現場でどのようにかけ算を教えているか？また、かけ算の導入方法や、かけ算順序について、激しい論争がある事を知らずに、推測で語っていた事を、お詫び申し上げます。
私のような、そういった教育現場を知らない保護者は大勢いると思うし、教育現場を知らなくても、議論の場に入っていっても良いのではないかと思います。
しかし、実際は、私のような何も知らない立場では、「そんなやつが議論するな、話題に入ってくるな」と言った態度、「そんなことも知らないのか」などという批判が多く、正直、「非難する人と話をしたくない」と思いました。
名のある有名な先生や、フォロワーが多い人が偉い訳ではありません。
（勿論、おいたんの肩書きが偉い訳でもありません。）
どんなに正しい事を言っていたとしても、非難から入るような人の言うことは聞きたくないし、今後も、聞くことはないでしょう。
（親しい人ならまだしも、全然知らない人や相手を馬鹿にするような人の話は聞きたくありません。）
相手を攻撃する人の周りには、攻撃する人たちが集まり、そういう人たちのところからは、私は、できる限り離れていたいと思います。
かけ算順序の話は、小2すんのテストを発端に、おいたんから聞いた話が面白く、誰かの役に立てるかもしれない…と思って描き始めた事です。
これらの記事で、数学的に間違いであることは記載しないよう努めておりますが、数学的に間違いがありましたら、コメント欄でご指摘ください。
（※ただの誹謗中傷は受け付けません。また、教育的にどうか？という話は推測に過ぎず、正確ではないため、お答えできません。）
かけ算順序問題は、問題を切り分ける必要があると思う
1掛け算の順序によって、まとまりの数への理解が進むのか？
数と日本語の問題。
2順番が違うと×（バツ）にするのか？
理解度を測る物差しの妥当性問題。
教育システムの問題。
3掛け算を、どう定義し、表記するか？
数学、言語の問題。
4掛け算の順番を入れ替えても、結果は同じなのか？
数学の問題。
5教育も色々な見方で行われている
何がねらいの教育か、カリキュラムの問題。
…などの問題があり、切り分けて考える必要があると思います（推測）。
しかし実際は、全て1つの問題と捉えている場合が多く、この漫画の当初の流れも、最終的には、数学的な問題と、教育的な問題を織り交ぜて展開しようとしていました。
今は、数学の話しかしていません。
教育問題は私の推測であるため、正しい知識ではない、と判断した為です。
また、当初、おいたん（兄）から聞いた話から、漫画の構成を大幅に変更したのは、2日に1回更新では、誤解を与える可能性がある為です。
誤解を極力減らすために、ストーリー展開が早まっただけで、内容に変更はありません。
（批判的なコメントや、漫画に対する否定が原因で内容を変更した訳ではなく、誤解が広まりそうなコメントを頂いたので、展開を早める構成にしました。）
尚、教育的な話は、こちらのツイート↓が参考になりましたので、こちらをご覧いただくことをお勧めします。
順序Ａと順序Ｂ
小学校の算数では、かけ算は、式を〈１つ分×いくつ分〉の順序に固定して、教えられている。この順序固定を演算の非可換性と誤認し混同する人が多い。
#掛算 #超算数 #算数 #算数教育 #かけ算の順序 #かけ算 #交換法則 #可換性 #非可換性
— kistenkasten723 (@flute23432) October 3, 2021
以上です。
次回から本編に戻ります。
