目次

こんにちは。しらこです。
前々回のお話で、「掛け算はどれで定義してもよい」というお話をしました。
ということは…

「2×3」も「3×2」も、「同じ!!」って言ったの、合ってたじゃん!!
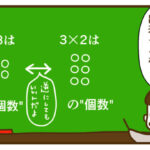
2×3も3×2も、当たり前?

何故ならあの時、「当たり前」となる根拠を説明出来なかったでしょ?
「あの時」の私の解答↓
↑「2×3」も「3×2」も「答えが同じ」と解答している。
これは、「答えを計算している」ということ。
この時、本当に「2×3=3×2」の根拠が分かっていたら、こう説明出来る。↓

同じ並びを、どう数えても一緒だから。
数え方が変わっても、そこにある"数"は変わらない。
だから、「掛け算は入れ替え可能」なんだねぇ。。。

教科書の行間をしっかり読んで、自分の頭で理解することが大切なんだよ。


↑かけ算を「2×3=2+2+2」と、累加で定義した以上、可換は当たり前ではない。だけど…というお話。

【超重要な注1、2】
数学を議論する際のお話です。
小学生は、「九九がそうだから」や、「計算結果が同じ」等も、立派な根拠になると思います。

「これ以上は説明出来ない」事柄


など、「当たり前」と思える様な事をどんどん突き詰めていくと、最終的に「これ以上は説明できない」事柄になる。

1 一般に通用する道理。
2 数学で、論証がなくても自明の真理として承認され、他の命題の前提となる根本命題。
3 自明であると否とを問わず、ある理論の前提となる仮定。


(公理なんて言葉、初めて聞いた…)

数学的帰納法…。
習った記憶はあるが、すっかり忘れている。
何だったっけ????
数学的帰納法(すうがくてききのうほう、英: mathematical induction)は証明の手法の一つ。自然数に関する命題 P(n) が全ての自然数 n に対して成り立つ事を証明するために、次のような手続きを行う[注 1]。
1. P(1) が成り立つ事を示す。
2. 任意の自然数 k に対して、「P(k) ⇒ P(k + 1)」が成り立つ事を示す。
3. 1と2の議論から任意の自然数 n について P(n) が成り立つ事を結論づける。
何だか難しそう??
いいえ、とてもとても簡単です。そしてそれは次のお話…。

高校の時、数学的帰納法で挫折した人や、今、高校生の人も、見てみてね。

え?そんな事???って言うくらい、拍子抜けする内容だから!!(多分)
こぼれ話
「2×3」も「3×2」も同じなら、どっちかに統一すれば良くない??
「2×3」と「3×2」に"違いが全くない"なら、もういっそのこと、どっちかに統一してしまえばよくないですか?
例えば、「数字が小さい方を前に書く」というルールにしたら、「3×2」って書くことがなくなり、常に「2×3」と書くことになる。

そしたらかけ算順序問題も一気に解決!!
九九表だって、逆の部分、覚えなくていいから、九の段だったら、「9×9=81」だけ覚えればいいし、めっちゃラクじゃん!!
いい考え!!

何故、このような表記ではダメなのでしょう?
実は答えはもうこのブログ内のどこかに出ているんだけど、また後日、(もしかしたら演算や実用上の問題を交えて)詳しくリライトします。


(注意:あくまでも数学のお話です。教育上云々の話ではありません。)
【2022/03/17追記↓】
何故、九九表の表記を半分だけ、とか、掛け算が交換可能なら片方だけ覚えればいい、としちゃダメなの?
何故なら、掛け算は演算だから。
数学において、二項演算(にこうえんざん、英: binary operation)は、数の四則演算(加減乗除)などの 「二つの数から新たな数を決定する規則」 を一般化した概念である。二項算法(にこうさんぽう)、結合などともいう。

例えば、
パンツを履いてズボンを履く。
ズボンを履いてパンツを履く。
パンツを先に履くか、ズボンを先に履くかで、見た目が変わる。
見た目に注目するのであれば、非可換(交換できない)。
でも、パンツとズボンを履いた時の「重さ」が知りたい。
のであれば、パンツを先に履いても、ズボンを先に履いても、重さは同じ(重さは可換(交換可能))。
見た目は関係ない重さを知りたかったとしても、パンツを先に履くか、ズボンを先に履くかという、どっちの概念も存在する訳で、どちらかがなくなるわけではない。
掛け算は可換(交換可能)だからと言って、どちらかの表記をなくせば良い、ということにはならないのです。

この例え話で逆に分かりにくくなる人もいるだろうし、あくまでも、私の認識、私が理解するために出した例え話なので、スルーしてください。

私は8×5を頭の中で「ゴハシジュウ」って考えて答えを出してるよ。
でも、自分が頭の中で「ハチゴ(8×5)」を使わないからと言って、他人が「ハチゴ」を使わないかどうかは分からないよね。
九九表を覚えることで、「掛け算は可換なんだ!!」って気づく人もいるだろうしね。

因みに、日本では昔、半九九で教えられていたそうです。
そして総九九になったのも、演算が理由ではなく、外国が総九九だったから取り入れたそうな。

総九九であることに、何の違和感も疑問もなかったけど、半九九だった時代もあったんだねぇ。(総九九、半九九って言葉があるのも知らなかった)
この辺りも調べてみると面白そうだね!!
気になる人は調べてみてね。

お風呂で九九を覚えるの、結構いいよ!!
コウ(幼稚園年中)も面白がって覚えてます。

![学校は掛け算を[まとまりの数]×[個数]で教えている【掛け算の順序2話目】](https://snsnblog.com/wp-content/uploads/2021/12/1-1-1-150x150.jpg)







