これは、小2すん(息子)のテストが発端となり、おいたん(兄)から聞いた話が面白かったので、漫画にしました。
ここだけ(2話目だけ)見ると、誤解が生じる恐れがあるので、是非、最後まで読んでいただければと思います。
学校教育に関する議論とは、無関係です。
こんにちは。しらこです。
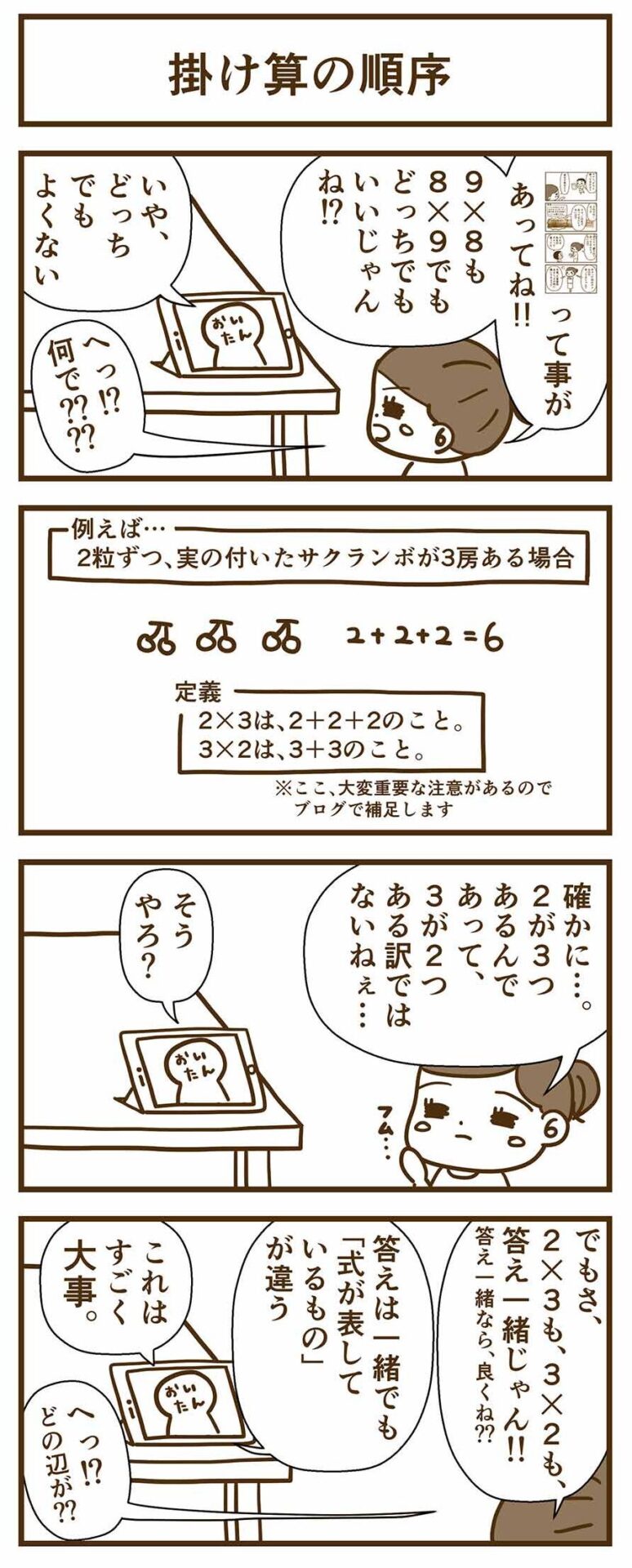
掛け算の順序、どっちでもいいと思っていませんか?
掛け算の順序は、人によってはどっちでもいいことかもしれませんが、"まとまりの数"の取り扱いがよく分からない人にとっても、「どっちでも良い」と、言い切ってしまっても良いのでしょうか…??
<注意>
勿論、"まとまりの数"の取り扱いが苦手であっても、掛け算の順序を固定する必要がない人はいるので、苦手な人全員に通用するものではありません。




何で????
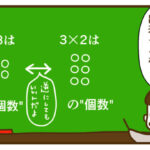
サクランボの例
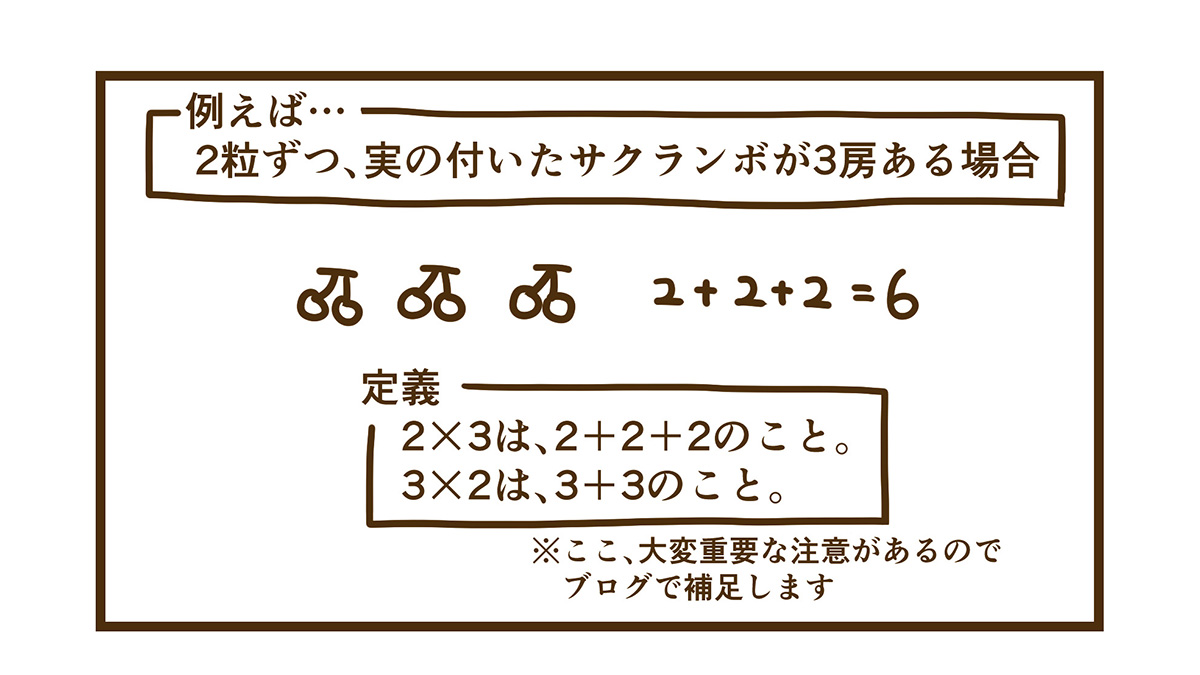
掛け算の定義は、乗法-Wikipediaでも、↑このさくらんぼの例のように、累加で定義されています。
※大変重要な注意(教科書は、累加で定義していない)
厳密には、すん(息子)の教科書には、「掛け算を累加で定義しましょう」と記載されていません。
教科書7ページ目に、「足し算で求めることができる」と書かれているだけです。
(↓教科書7ページ目)

すん(息子)の話を聞くと、「2×3は、2+2+2のこと」という認識であり、すんの友達(他のクラスの子)も、「2×3=2+2+2と教えられた」という認識でした。
このことから、私は、累加で教えられている…と、解釈しました。
しかし、先生がどう教えたか?と言われると、実際のところは分かりません。
あくまでも、すん(息子)や、すんのお友達が、「2×3=2+2+2である」という認識です。
もっと詳しく知りたい人はこちら
例えば…
2粒ずつ実の付いたサクランボが3房ある場合。
2粒が3房あるんであって、3粒が2房ある訳ではない。
だから、式は、
「2(個のまとまりが)×3(つある)」となります。

小学校では、このように、「(まとまりの数)×(何個)」というように習います。
(↓実際にすんが使っている教科書。「1つ分」×「いくつ分」のように、左側が必ず「1つ分」になっている。)


だから、文章問題だと、「ちゃんと文章を理解して、問題解いてる??式が逆だったら、問題の意味、分かってないよね?」ってなるんだよ。

ここで補足すると、分かりにくくなりそうなので、別のところ(掛け算の順序5話目)でお話します。
答えが合ってるなら、式も正解で良くないか??
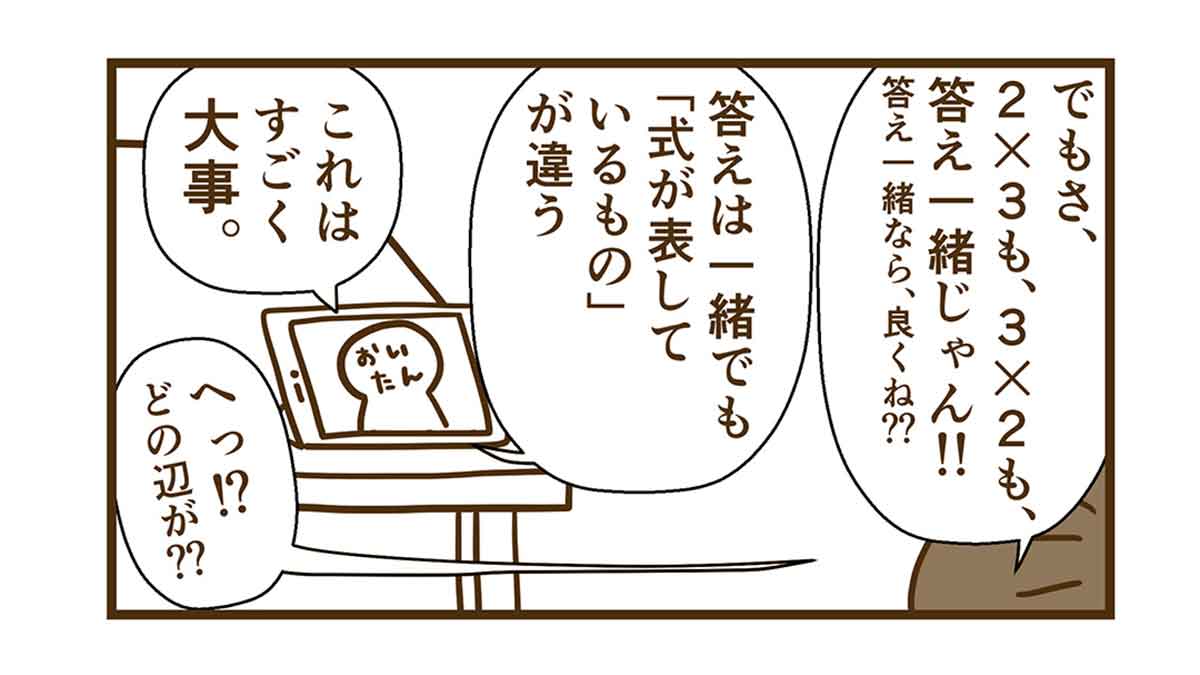

答えがあってるんだから、掛け算の式なんて、どっちがどっちでも良くね!?

これは、すごく大事。

どの辺が大事なん??
どう言う事??
と言う事で、詳しくはまた次回…。
式に意味はないなんて言う人もいるかもしれないけど、ちゃんと意味があるんだよ。

なんか聞いた事ある…くらいに思ってくれればいいかな。

あのねぇ〜、ボクねぇ〜、大きくなったらサンズと戦いたいの〜。
次回予告

(↑この人は、「おいたん」です)
「概念」は、「それはどういうものか」についての共通の認識を指します。

なんか、分かってきたような。。。まだよく分からんような。。。
「おいたん」がついに具体化!?(そんなこたぁ〜どーでもいい)
…と言うことで、続きはまた次回。。。
↑私の故郷、愛媛のお菓子。母恵夢。

「博多通りもん」とか、「なごやん」に似てるかも…。
母恵夢は色んな種類があって、季節限定商品とかも色々あって、美味しいよ!!
りんご味や、くるみショコラなんてあるんだねぇ〜。
お試しあれ!!