こんにちは。しらこです。
掛け算順序の話を描いたことで、色々な意見が寄せられるので、私の見解をまとめました。

何故か?ってところをブログに書くね!!

私の解釈と他人の解釈は違うし、気になったら、自分で考えてみてね。
目次
- 掛け算順序問題とは?
- さくらんぼの例【掛け算順序2話目より】
- テストでマルでも"まとまりの数"を理解しているか判別できない例
- 学習指導要領には何て書いてる?
- 「一つ分×いくつ分」と順序を固定して教えてはいけないの?
- この掛け算順序シリーズで言いたかったことは何?
- 一つ分(被乗数)×いくつ分(乗数)で考えるのは間違いなの?
- 一つ分(かけられる数)×いくつ分(かける数)で子供達に教えるのは有用?エビデンスは?
- 掛け算の順序はどっちでも良いけど、じゃあ掛け算の順序を少しも固定しないで、"まとまりの数"の理解を促すにはどうすればいいの?
- 日本語の語順(主語+述語)を考えると、「いくつ分×一つ分」と考えた方が、分かりやすいと思う
- 掛け算に順序はないけど、掛け算に順序はないって教えた方が有用であるっていうエビデンスはあるの?
- 掛け算順序論争について思うこと
掛け算順序問題とは?
掛け算順序問題とは?

↑すん(息子)の実際のテスト。
9×8でも8×9でも問題ないはずが、「9×8」の時、バツ(間違い)とされる。
何故、このような事が起こっているのか?
さくらんぼの例【掛け算順序2話目より】
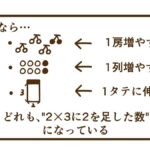
学校では[まとまりの数]×[いくつ分]と教える
すんの教科書20ページ目
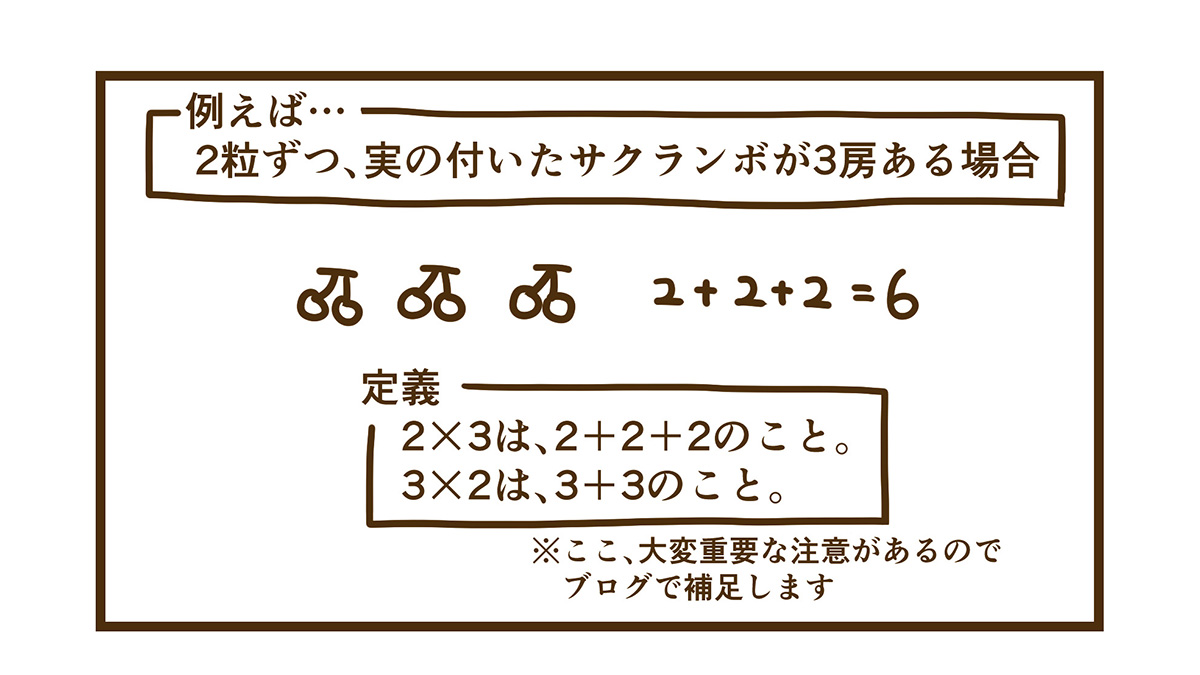

2粒ずつ実の付いたサクランボが3房ある場合、この状況だけみると、「2のまとまり」が「3つ分」とイメージしやすいと思います。(でも、イメージしにくい人もいるだろうね。)
この状況では、こう考える方が分かりやすく、想像しやすいので、「2×3」が正しい解答である、と思ってしまいがちです。

そう考える方が私も分かりやすいと思ったよ。
この考え方も正しい解法の一つだから、間違いじゃないよ。

そしてこの状況は、3粒ずつ実の付いたサクランボが2房あるわけではありません。
3粒ずつの実が2房なら、3×2=3+3と想像しやすく、式は「3×2」が正解となり、「2×3」は誤りである。
とされ、"まとまりの数"を考える時は、掛け算の順序を考えましょう、となり、あたかも、掛け算に順序があるように取り扱われているのです。

だって、掛け算はどっちがどっちでもいいんだもの。

「3粒ずつ実の付いたさくらんぼ2房」は、
確かに状況が違うけど、総数"6"だし、状況が違ったとして、2×3でも3×2でもどっちでもいいんだよ。
この場合、どっちがどっちの状況か?って大事じゃないからね。
状況が違うね、だから何?って話なんだよ。

その状況が、こういう式で表せるかな?と考えてイメージすることはできるけど、数式自体は、その時の状況を表したりできないからね。
配り方を変えると「2×3」にも「3×2」にもなる↓

「3人に2個ずつ配る」という問題は、①、②の配り方以外にも色々な方法(解釈)があります。
3個ずつ配って、後で3引いてもいいし、1つずつ数えてもいい。
このように、状況が違っても同じ数式で表すことができ、式は、どれも正解になります。
他にも、こう考えれば同じ数になるって証明できるよね
「2粒ずつの実が3房」と「3粒ずつの実が2房」、状況は違いますが、どちらも、みを取って数えたらどうでしょう?
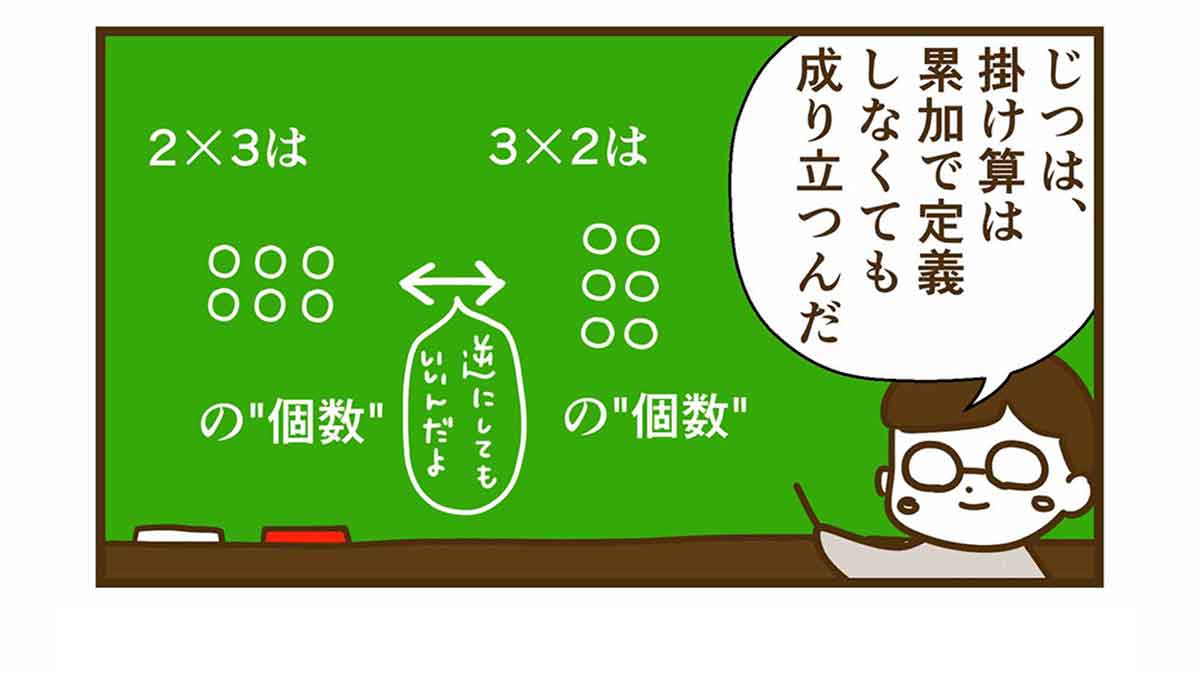
「2のまとまりが3つ」としても、「3のまとまりが2つ」としても良く、答えは「6つ」。
どちらの状況だったとしても、みを取って数えることができ、「2×3」でも「3×2」でも成り立つことが分かります。

このように、文章問題だったとしても、解釈の仕方は色々あり、「2×3」と「3×2」の式から、子供達が、"まとまりの数"を理解しているか?していないか?を測ることは出来ないのです。

教科書の導入がこういう「状況」や、絵に描かれたような「場面」だと、その場面のみ、掛け算が使えると思い込む子や、状況によっては唯一正しい掛け算の式が存在する…と思い込む子も出てくる可能性があります。
さくらんぼの問題だと、房から実を取って考えてもいいし、実を面積と捉えて考えてもいい。

さっきも言ったけど、より抽象化して考えられるようになることは数学にとってとても大事なことだよ。


式と状況を紐付ける必要は全然ないから、テストでバツにする必要はないよね。
テストでマルでも"まとまりの数"を理解しているか判別できない例
掛け算順序問題におけるサンドイッチ法
という問題が出された時、
5(個)×3=15(個)
というように、答えが「◯個」になるならば、「個」が付いた数で「サンドイッチ」になるように書く。
という方法の事。
この方法だと、「一つ分×いくつ分」という式が作れるので、テストでマルはもらえるけど、マルを貰えても、"まとまりの数"を理解したことになるでしょうか?

このように、テストでマルであっても、バツであっても、子どもが"まとまりの数"を理解しているかどうか?を測ることは出来ません。


"まとまりの数"を理解したかどうか?なんて本人でないと分からないのに、それをテストでどうやって判断するんですか?
少なくとも、「掛け算は可換である」という事は正しい事実であり、正しい事実ならば、「2×3」でも「3×2」でも、どちらも正しくないと、おかしくないですか?

学習指導要領には何て書いてる?
学習指導要領(がくしゅうしどうようりょう)は、文部科学省が告示する初等教育および中等教育における教育課程の基準である。

この学習指導要領を見ると…
乗法に関わる数学的活動を通して,次の事項を身に付けることができるよう指導する。
ア 次のような知識及び技能を身に付けること。
(ア) 乗法の意味について理解し,それが用いられる場合について知ること。
(イ) 乗法が用いられる場面を式に表したり,式を読み取ったりすること。
(ウ) 乗法に関して成り立つ簡単な性質について理解すること。
(エ) 乗法九九について知り,1位数と1位数との乗法の計算が確実にできること。

しかし、学習指導要領の解説には、掛け算の順序について触れられていました(長いので、引用の下にまとめてみたよ。)↓
ア 乗法が用いられる場合とその意味
乗法は,一つ分の大きさが決まっているときに,その幾つ分かに当たる大きさを求める場合に用いられる。
例えば,「1皿に5個ずつ入ったみかんの4皿分の個数」を求めることについて式で表現することを考える。
「5個のまとまり」の4皿分を加法で表現する場合,5+5+5+5と表現することができる。
また,各々の皿から1個ずつ数えると,1回の操作で4個数えることができ,全てのみかんを数えるために5回の操作が必要であることから,4+4+4+4+4という表現も可能ではある。
しかし,5個のまとまりをそのまま書き表す方が自然である。
そこで,「1皿に5個ずつ入ったみかんの4皿分の個数」を乗法を用いて表そうとして,一つ分の大きさである5を先に書く場合5× 4と表す。
このように乗法は,同じ数を何回も加える加法,すなわち累加の簡潔な表現とも捉えることができる。
言い換えると,(一つ分の大きさ)×(幾つ分)=(幾つ分かに当たる大きさ)と捉えることができる。
また乗法は,幾つ分といったことを何倍とみて,一つ分の大きさの何倍かに当たる大きさを求めることであるという意味も,併せて指導する。
このときも,一つ分に当たる大きさを先に,倍を表す数を後に表す場合,「2mのテープの3倍の長さ」であれば2× 3と表す。
なお,海外在住経験の長い児童などへの指導に当たっては,「4×100 mリレー」のように,表す順序を日本と逆にする言語圏があることに留意する。
ここで述べた被乗数と乗数の順序は,「一つ分の大きさの幾つ分かに当たる大きさを求める」という日常生活などの問題の場面を式で表現する場合に大切にすべきことである。
一方,乗法の計算の結果を求める場合には,交換法則を必要に応じて活用し,被乗数と乗数を逆にして計算してもよい。
乗法による表現は,単に表現として簡潔性があるばかりでなく,我が国で古くから伝統的に受け継がれている乗法九九の唱え方を記憶することによって,その結果を容易に求めることができるという特徴がある。イ 乗法の式
乗法が用いられる具体的な場面を,× の記号を用いた式に表したり,その式を具体的な場面に即して読み取ったり,式を読み取って図や具体物を用いて表したりすることを重視する必要がある。
その際,乗法の式から場面や問題をつくるような活動も,乗法についての理解を深め,式を用いる能力を伸ばすために大切である。
式に表す指導に際しては,「1皿に5個ずつ入ったみかん4皿分の個数」というような文章による表現,○やテープなどの図を用いた表現,具体物を用いた表現などと関連付けながら,式の意味の理解を深めるとともに,記号 × を用いた式の簡潔さや明瞭さを味わうことができるようにする。
式を読み取る指導に際しては,例えば,3× 5の式から,「プリンが3個ずつ入ったパックが5パックあります。プリンは全部で何個ありますか。」という問題をつくることができる。
このとき,上で述べた被乗数と乗数の順序が,この場面の表現において本質的な役割を果たしていることに注意が必要である。
「プリンが5個ずつ入ったパックが3パックあります。プリンは全部で幾つありますか。」という場面との対置によって,被乗数と乗数の順序に関する約束が必要であることやそのよさを児童が理解することが重要である。
このようにかけ算の式を具体的な場面と関連付けるようにすること,さらに,読み取ったことを,○などの図を用いたり,具体物を用いたりして表現することが,式を読み取る能力を伸ばすためには大切である。ウ 乗法に関して成り立つ簡単な性質
「内容の取扱い」の(4)で「主に乗数が1ずつ増えるときの積の増え方や交換法則を取り扱うものとする」と示されているように,ここでは,乗法に関して乗数が1増えれば積は被乗数分だけ増えるという性質や,乗法についての交換法則について児童が自ら調べるように指導する。
乗法九九を構成するときに乗数が1増えれば積は被乗数分だけ増えること,乗法についての交換法則などを活用し,効率よく乗法九九などを構成したり,計算の確かめをしたりすることも大切である。ここで「主に」と書かれているのは,児童の実態に応じて,図などと関連付けながら,乗法についての結合法則や分配法則に基づいた考えに触れてもよいことを意味している。エ 乗法九九
乗法九九は,以後の学年で取り扱う乗法や除法の計算の基盤となるものとして必要なものである。
したがって,乗法九九を構成したり理解したりする際には,体験的な活動や身近な生活体験などと結び付けるなどして指導の方法を工夫することが重要である。
また,どの段の乗法九九についても十分に習熟し,確実に計算することができるようにするとともに,それらを生活や学習に活用することが大切である。
乗法九九を生活や学習の場面で活用することによっても,技能の習熟が図られる。
私なりに要約すると…
4×5ができなくもないけど、5×4と考える方が自然だよね。
(一つ分)×(いくつ分)=(幾つ分かに当たる大きさ)と考えられるね。
海外歴が長い子は、「一つ分×いくつ分」が逆の場合もあるから、注意してね。
「一つ分×いくつ分」は、日常生活の場面を式で表現する場合に大切だよ。
だけど、計算結果を求めるときには、掛け算の交換法則を使って、逆にしてもいいよ。
3×5を教える時、「プリンが3個ずつ入ったパックが5パックあります。プリンは全部で何個ありますか?」という問題が作れるけど、
「プリンが5個ずつ入ったパックが3パックあります。プリンは全部で何個ありますか?」ではないよね。ここ、重要だよ。
だから、「一つ分×いくつ分」の約束が必要なんだよ。


掛け算を累加で定義すると、可換は自明ではない(証明が必要)という意味だよね。

プリンが3個ずつ入ったパックが5パックあります。と、
プリンが5個ずつ入ったパックが3パックあります。では、
状況が違うね、だから何?という話だよ。
どちらも総数は同じだよね。

実際、順番にした方がわかりやすいよ、的なこと書かれてるし。
「一つ分×いくつ分」と順序を固定して教えてはいけないの?
「一つ分×いくつ分」について、否定的な感じで書きましたが、相手の理解が進むのなら、私は、「一つ分×いくつ分」と固定して教えても良いと思います。
ただし、「一つ分×いくつ分」が、あくまで"まとまりの数"の理解を進めるために用いるものであって、教える側が、「一つ分×いくつ分」の式をもって、"まとまりの数"の概念の理解が進んでいるかを判断するものではない、と私は思います。
「一つ分×いくつ分」で考えたとき、そう考える方が分かりやすい人もいれば、分かりにくい人もいるでしょう。
分かりにくい人には別の方法で教えてあげればいいだけのこと。
全員が「一つ分×いくつ分」で理解が進むか?というと、そういうわけではないと思います。

テストでバツにまでする必要はない、っていうのが私の意見です。
すんに、「2×3も3×2も答え同じだからどっちでもいい」って言ってみた



2粒ずつ実のついたさくらんぼが、3房あります。
実は全部でいくつでしょう?

2×3で6!!

すんちゃん、よく分かってるね!!



だって、2つのまとまりが、3つだから、2×3じゃないとダメじゃん!!











この段階でも、「一つ分×いくつ分」で教えてるから、私(ママ)は、掛け算を固定して教えています。
そしてすん(息子)は、その方が分かりやすそうでした。


勿論、"まとまりの数"の理解を深めるためなら、掛け算の順序に拘る必要はないよ。
掛け算の順番に注目するんじゃなくて、相手が、分かっているか?分かっていないか?に注目した方がいいと思うよ。
そして数日後…。
すん(息子)に、こんな問題を出してみました。
こんな問題出してみた


すん(息子)の、最初の解答は、これ↓






ママ、待って!!
そして次はこれ↓。





だって、全部で何個でしょう?だから、答えが"6"なら正解なんでしょ?

全部の数を聞いてる問題だから、本当はどんな式でも答えが"6"なら正解なんだよ。

不安になってきた…。

「答えが全部同じ」っていうの、8-2も、答え「6」になるけど、式は「8-2」でもいい?

だって、「8-2」は、数えても「8-2」にならないもん。
それに、文章問題は、文章問題に出てくる数字を使いなさいって先生が言ってた!!

この問題は、「3枚のお皿にリンゴが2個ずつのっています、全部でいくつでしょう?」だもんね。
すん(息子)はまだ割り算を習っていませんが、答えが"6"なら、18÷3でもいい。
8-2などの引き算でもいい。
ただし、8-2や18÷3とする場合、どういった解釈をしたのか?が大事になる。
ここは、「3枚のお皿に、2個ずつリンゴが乗っていると、全部でいくつでしょう?」なので、その問題を読んで、論理的に式を求めることができるのなら、18÷3でも、8-2でもいい。

色々な解釈をする事は、数学には大事だからね。
6枚のお皿に、2個ずつりんごが乗っています。りんごは全部でいくつでしょう?
という問題だったら、3×4でも4×3でも構わない。
3人に49個ずつ飴を配りました。全部でいくつ配りましたか?
この問題、わざわざ49×3(もしくは3×49)しますか?(勿論、する人もいる)
頭の中で、50×3して、3引く(147)ってしませんか?

もし、式変形するだけであれば、そこに解釈は必要ないけどね。

掛け算順序固定反対派の人たちは、ここは認めてるのかな?(某数学者の人が認めてるのは知ってる)


答えが分かってる、とか、掛け算の交換法則を知っている、っていう理由でOKなら、全部マルだね。

イコールで結べるかどうか分からない問題は証明が必要になるよね。
「◯×△」と「□÷☆」を、イコールで結びたいなら、証明しないといけないよね。
掛け算のテストで順序にバツが付けられる。
順序なんてどっちでもよく、答えが合っていればいいと言うのなら、どこまで許容できますか?
この掛け算順序シリーズで言いたかったことは何?
数学の面白さを伝えたい、掛け算はこうやって考えることもできるよね、と言いたかったです。
(決して、掛け算に順序がある、といいたかった訳ではありません。)
掛け算順序1話目が、すん(息子)のテストがきっかけだったので、掛け算順序論争をするのかと勘違いした人、すみません。
小学校に関する掛け算順序について、議論する気はありません。
1話目で、すん(息子)の話をし、ペルソナはすん(息子、小2)と見せかけて、2話目以降は私(ママ)。
ペルソナが私(ママ)であっても、「掛け算を累加で定義すると可換は自明ではない」という事は、知る必要もないし、知らなくていい。
ただ、私が知りたくて、面白かったから、描き始めました。

何度でも言うけど、小学生にそんな事、求めてないよ。

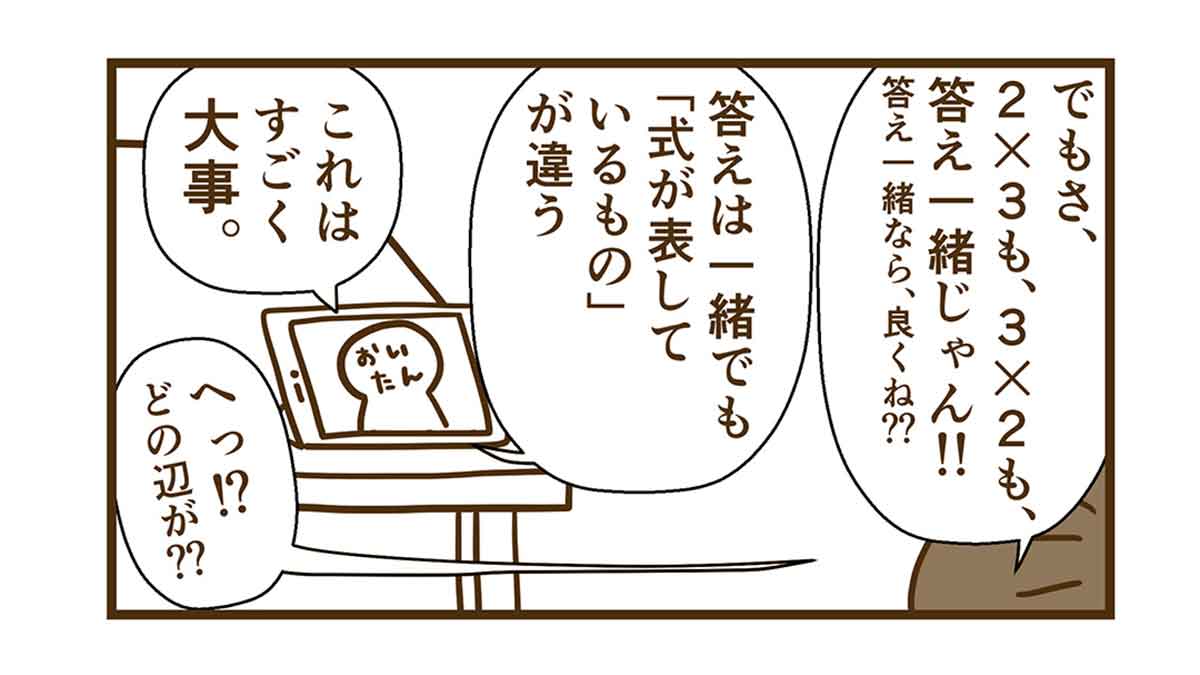
↑ここは、掛け算を累加で定義すると、可換は自明ではないため、答えが合っているだけではダメで、私の解答が"違う"となります。

「掛け算は可換か?非可換か?」を学んでいる人以外は、どっちでもいいしね。

だってさ、本当にどっちがどっちでもいいなら、「A×B=B×A」なんて式すら必要ないし、存在しないでしょ?
「A×B=B×A」と言う式が存在する以上、何かしら理由があるんだよ。

「式が表しているものが違う」というのは、そういうことだよ。
「2×3」は、ただのラベル(名前)であって、「2×3」に、どういった意味をもたせるか?それが定義なんだよ。
式が場面を表す、という解釈の話ではないよ。

私も最初は全然分からなかったけど、そっか〜!!おもしろ〜い!!ってなったよ。
数学って、面白いね!!
一つ分(被乗数)×いくつ分(乗数)で考えるのは間違いなの?
いいえ。間違いではありません。
学校で習う「一つ分(被乗数)×いくつ分(乗数)」だって、正しい解法の一つです。
有効であればそれを用いればいいし、必要なければ使わなければいい。という話です。
掛け算順序論争の否定派の人たちが言っているのは、「一つ分×いくつ分」も「いくつ分×一つ分」も正しいのに、「一つ分×いくつ分」のみが正しい、唯一の解法だと主張するのは間違っている、と言っています。

全部でいくつ?って聞かれても、色々な解釈があるもんね。
式に答えがあるように採点されると、その式以外は「間違い」と思っちゃいそうだもんね。
一つ分(かけられる数)×いくつ分(かける数)で子供達に教えるのは有用?エビデンスは?
エビデンス(科学的根拠)や、何十件も検証した結果は示せませんが、
私自身がそうであること、また、周りの話や、今回、すん(息子)に問題を出してみて、改めて「一つ分×いくつ分」で考える事は有効だと実感しました。

私(しらこ)は小学生時代、「一つ分×いくつ分」と教えてもらわなかった

2×3も3×2もどっちも一緒って教えられてたから、子供のテスト見るまで、掛け算に順序があるなんて考えたこともなかったし。
でも、おいたんに言われて、2×3は、2+2+2だね、3×2は3+3だよね、言われて、なるほど!!って思ったし、小学校時代にそうやって教えてもらえていれば、もっと"まとまりの数"の理解が深まって、分かりやすかったんじゃないかなぁ?って思ったよ。
掛け算の順番なんて、どっちがどっちでも良いけど、なんで式はバツなの?って子供に聞かれた時に、"まとまりの数"がちゃんと考えられているかな?
一つ分のまとまりはいくつ?それが何個分?って聞いて、それで"まとまりの数"の理解が進めば、それで良いんじゃないかな?と思います。

私もそうだし、掛け算なんて、どっちがどっちでも答え一緒だからいいじゃん!!っていうのは、実際正しいし。
だけどこの、「掛け算はどっちがどっちでも答えが同じ」だからいいって言うの、子供にちゃんと説明できる?
"まとまりの数"の理解があやふやな人に、そう言っちゃうと、逆に混乱するかもしれないよ?
そこら辺は、よく考えて教えてあげたいなーと思います。

「一つ分×いくつ分」だって、正しい解釈の一つなのにね。
掛け算の順序はどっちでも良いけど、じゃあ掛け算の順序を少しも固定しないで、"まとまりの数"の理解を促すにはどうすればいいの?
これは私が疑問に思っていることです。
掛け算の順序はどっちでも良い、掛け算順序固定否定派の、「一つ分×いくつ分」が害悪でしかない、と思っている人たちに聞いてみたいです。
例題
4/5分は何時間ですか?
4/5時間はなん分か?を考える時、
"1時間あたり"60分で、それの4/5倍だから…
60×4/5=48(分)
これを基に考えると、
4/5分は何時間か?は
"1分あたり"1/60時間で、それの4/5倍だから、
1/60×4/5=4/300=1/75(時間)
となる。
1分がa時間だと分かった。
ならあとは、aを何倍かすれば良い。
こういう、"1分あたり"、"一人あたり"、"〇〇あたり"の概念が理解できていれば、abでもbaでもいいし、慣れたら機械的にしても良い。
と、教える方が、私は理解しやすいんじゃないかな?と思いました。

この問題を解く時、
4/5時間はなん分ですか?は、
4/5(いくつ分)×60(1時間あたり)=48
と考え、
4/5分は何時間ですか?を、
4/5×1/60=1/75
と考えるのも勿論ありだと思います。
(この場合でも、「乗数×被乗数」として(掛け算の順番を固定して)教えることになってるけどね。)
これとは別に、掛け算に順序はない、どっちがどっちでもいい!!と主張する人は、
4/5時間はなん分ですか?は、
60×4/5=48(分)
と教えた時、
4/5分は何時間ですか?を、
4/5×1/60=1/75
と教える場合、どうやって教えますか?
これ、逆でも構いません。
4/5×60=48
と教えた時、
4/5×1/60=1/75
と教える場合、どうやって教えますか?
掛け算は交換可能、順番なんてどっちがどっちでも良い…と知っていても、私なら、混乱するし、"〇〇あたり"の理解を深めるためには、固定した方が分かりやすいんじゃないかな?と思います。
少なくとも私は、このような時間の問題や、速さの問題で子供がつまずいた時、"〇〇あたり"を考えると分かりやすいよ〜、と、教えたいと思っています。

日本語の語順(主語+述語)を考えると、「いくつ分×一つ分」と考えた方が、分かりやすいと思う
先ほどの例題でも出しましたが、「いくつ分×一つ分」としても、「一つ分×いくつ分」としても"まとまりの数"の理解が深まるのなら、どっちでも良いと思いますが、日本語を考えると、「いくつ分×一つ分」と教えた方が、理解されやすいんじゃないかな?と思います。
少なくとも私は、日本語でコミュニケーションをとっているので、「いくつ分×一つ分」の方が、理解しやすいし、説明しやすいです。
掛け算に順序はないけど、掛け算に順序はないって教えた方が有用であるっていうエビデンスはあるの?
これは私も分からないので、そういう論文やデータがあれば、教えていただきたいです。
また、もし、〇〇%有用である、と分かったとして、それが100%でないならば、それは、掛け算に順序はない!!と、数学的に正しい事実を教えても、人によってはそれが理解できない、分かりにくい、ということになるんじゃないでしょうか?
エビデンスは大事だと思いますが、教育に絶対はないと思います。
掛け算順序論争について思うこと
同じことを何度も書きますが、この掛け算順序シリーズは、
おいたん(兄)から聞いた話が面白く、数学の面白さを広めたかった話です。
掛け算(高校までの普通の掛け算)を定義する方法は一通りではなく、定義の仕方によって可換性は小学生にも自明になります。
こういった、ある定義や枠組みで証明することが難しくても、同値な別の定義や枠組みを用いることで証明できる事は数学ではよくあるそうで、身近にもそんな例があって面白いよねってことを伝えたかった記事です。
また、子供がテストでバツをもらった時に、こう言う考え方でバツになってるんだよ、ということを伝えたかった話です。
だからと言って、「掛け算に順序がある、掛け算の順序を固定し、強制的に教えるのが大事」というのを広めたかった訳ではありません。
この記事にも書きましたが、
「掛け算の順序を固定して指導する」という方法は、学習指導要領には書いていません。
(「一つ分×いくつ分」で考える事は大事だよ、とは書かれていますが、「一つ分×いくつ分」の順に固定して指導せよ、とは書かれていません。)
テストでの判断は、現場の先生に任せられている、という現状だと思います。
とはいえ、実際は同調圧力等により、現場の先生の中にも、掛け算の順序が違う事で、泣く泣くバツを付ける人もいれば、バツをつけられて、算数が嫌いになる子供もいることでしょう。
もしかしたら、そんな事は考えず、片方の式しか書かれていない答案を見て、何の疑問も持たず、機械的にマル付けをしているだけかもしれない…。
掛け算の順序で正誤を判断されるということは、まとまりの数(単位あたりの量)を理解している人にとっては、学校が掛け算の順序を求めているから、こう回答する…というような忖度をして、(数学的に正しくない理解を曲げてまで、丸をもらうために)掛け算の順番を式に書いていることになり、これは、科学にとってはプラスどころか、マイナスであるとすら思います。
そこは、掛け算順序否定派の人たちの考え方に同意します。
掛け算順序否定派の人たちが、世の中を変えようと訴え続け、しかし、優しい言葉の訴えでは全然世の中が変わらなかったので、凄い強い言葉で訴えるようになった…というのにも、理解は示せます。
しかし、ただ、理解は示せるだけで、私はそういう行動をしようと思いません。
そういった強い言葉で行動するのが正しいとは、私は思いません。
掛け算順序固定で教える事に一つもメリットがない、エビデンスもない…という人もいますが、一つもメリットがないというエビデンスもまた、ありません。(これは私の認識なので、既にあるようなら教えていただきたいです。)
【注意】
「掛け算順序を固定して教えることに」というのは、「掛け算順序固定を強制して教えること」という意味ではありません。
私は、メカニズムが分かっているからといって、そのメカニズムに合わないと無意味か?というと、そんな事は全然なく、また、そこが難しく、解明されていないところだと思っています。
こと教育に関して、入力と出力の間にはブラックボックスがあり、Aと入力したからと言って、Aの出力が出る訳ではない…ということを、理解しておく必要があるのではないかな?とも思います。
掛け算を「場面」で導入している部分、私は、掛け算を累加で教えていると思っていたし、子供たちも累加で教えてもらっているという認識でした。
(某数学者に強く批判されたので、修正しました。詳しくは【掛け算順序番外編】より)
ここでも、掛け算を累加で導入していない(入力)としても、子供は累加であると認識している(出力)ならば、それは掛け算は累加であるという教育ではないのか?と思います。
また、サンドイッチ法では全然無意味だ。というようなことも書きましたが、それも果たして本当に無意味でしょうか?
意味を理解せずやっていたとしても、ある日突然、「分かった!!」となる日がくることもあるのではないでしょうか。

期間を空け、2回、3回繰り返すことで、自然と紐解け、理解が進むこともあったよ。
勿論、理解が進まないこともあるけどね。
強い言葉を使って、掛け算順序を肯定する人も、否定する人も、このあたりのことをよくよく考えてみて欲しいと思います。
私は、掛け算順序擁護派でも否定派でもどちらでもありませんが、今回、この漫画を描いたことで、掛け算順序を擁護していると捉えられたようです。
実際、正しい解釈の一つとして、私なりに分かりやすく描いたので、それが、見る人にとっては、「掛け算の順序を固定することこそ正しい!!」と主張しているように解釈されたのでしょう。
そんなつもりは全然ありませんが、掛け算の順序を固定して教える事は、教えやすいし、理解されやすいのではないかな?とは思っています。
なので、掛け算の順序を固定することは害悪でしかない、一つもメリットがないという掛け算順序固定否定派の人たちには、
"まとまりの数"の取り扱いがあやふやな人に、掛け算順序を固定せず、"まとまりの数"の理解を、どうやって教えますか?
と、聞いてみたいです。

九九表覚えれば、「掛け算は入れ替えてもいいんだ〜」って気付くだろうし。
私これ、"掛け算"を教えてるんじゃなくて、"まとまりの数"の取り扱いを教えるために"掛け算"を使ってるんじゃないかと思うんだよね。
どう思う?

今も出てるのかな??
ポンジュース、美味しいよね!!



![学校は掛け算を[まとまりの数]×[個数]で教えている【掛け算の順序2話目】](https://snsnblog.com/wp-content/uploads/2021/12/1-1-1-150x150.jpg)